 |
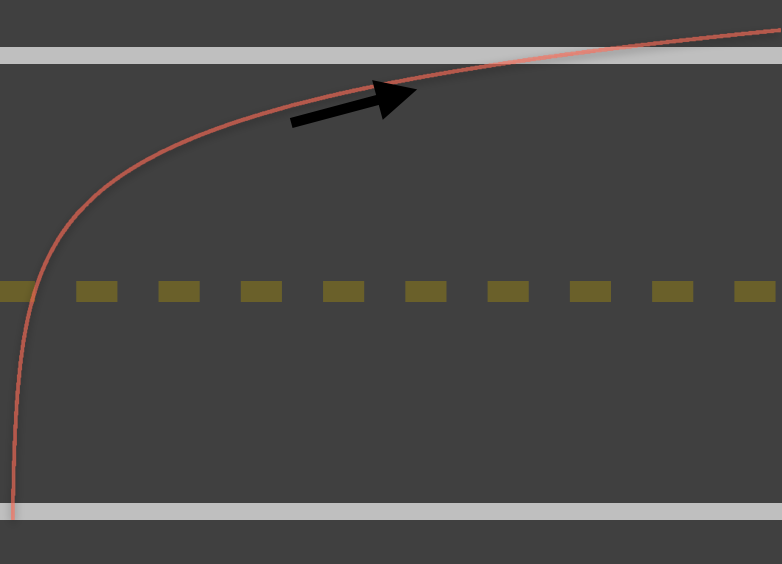
| こんな感じに(底はネピア数). |
- 車道の半分以上の領域を,速やかに渡り切ることが出来る.
- 反対側の歩道を歩く人々と,なだらかに合流できる.
車道と直角にy軸を置くことで,渡り始めをほぼ直角にすることが出来る. ここで,車道に直角な進路とは,車道横断最短経路を意味する. 車道の中央(センターライン)を越えた辺りから,徐々にその傾きは0へと近づく. これは,横断者が急な進路変更を行う必要の無いことを意味し,横断者自身の身体への負荷を最小限に抑えられることが期待される進路と成っている. 車道は自動車が走行しているため,速やかに渡り切ることが,安全上大切であることは言うまでも無いのだが,急いで横断した先に別の歩行者がいることを考慮せずして安全は語れない. 急いで渡ったために,反対側の歩行者と衝突してしまう事態は避けなければならない. そのためには次の2つの事柄を意識する必要がある.
- 他の歩行者は自分の進路を予測して行動する.
- 出来る限り長い間,他の歩行者の視界に入っていた方が良い.
驚くべきことに,LOG曲線は上2つの事柄を加味しても理想的な経路を提供してくれることに気づく. 傾きが徐々に0へと近づく,数学的な動きは非常に予測し易い. 微分不可能な動きは,非常にカオス的(人の脳が考えつく限りのランダムさであると考えるとこの言葉は適切で無いが...)であり,その経路は予測困難となる. 予測の出来ない動きは,長時間観察してもそのパターンを抽出することが出来ず. ましてそのような歩行者が近づいて来るとなると避けようが無い. 一方,LOG曲線は非常に美しく数学的な経路を提供するので,他の歩行者はその経路を予測し易く,時間の許す限り如何様にでも避けることが出来る. また,反対側の歩道に合流するときには,歩道と平行な直線へと漸近するため,他の歩行者は直角に進入する横断者より確実に長時間その横断者を視界に入れておくことが出来る. これは予測のし易さへと帰着する.
以上の事実を素直に受け入れるか,考え過ぎだと捨て去るかは,読み手であるあなたの意思にお任せするとして,私はこれほどまで横断に適した曲線は無いと唱える. 更に言えば,LOG曲線は横断のし易さのみに留まらず,道路状況に応じた選択ができるようにも成っている. これは底をパラメータとした選択であり,底の数を大きくするとより最短経路に近づくことが知られている. 車道を走っている車の数が多い時は,最短経路に近い,例えば底を10とした常用対数曲線に,一方車の数が少なく歩行者が多い時は底の小さなLog2(x)の曲線を経路として用いることで,よりスマートな車道横断となること誤りは無い.
75213831773823211
https://www.storange.jp/2014/01/log.html
https://www.storange.jp/2014/01/log.html
LOG曲線と車道横断
2014-01-12T18:29:00+09:00
https://www.storange.jp/2014/01/log.html
Hideyuki Tabata
Hideyuki Tabata
 200
200
200
200
 72
72
72
72
 72
72
72
72